dp문제는 역시나 딱 봤을때 떠오르지 않는게 문제다.
결국 힌트를 보고 풀었다.
https://school.programmers.co.kr/learn/courses/30/lessons/12971#qna
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다.
스티커_hb1jty.jpg
원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 하고 싶습니다. 단 스티커 한 장을 뜯어내면 양쪽으로 인접해있는 스티커는 찢어져서 사용할 수 없게 됩니다.
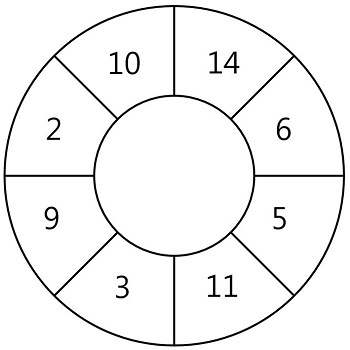
예를 들어 위 그림에서 14가 적힌 스티커를 뜯으면 인접해있는 10, 6이 적힌 스티커는 사용할 수 없습니다. 스티커에 적힌 숫자가 배열 형태로 주어질 때, 스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값을 return 하는 solution 함수를 완성해 주세요. 원형의 스티커 모양을 위해 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어 있다고 간주합니다.
제한 사항
sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.
해설
일단 dp가 필요한 이유는 각 단계마다 최댓값을 갱신하면서 계산해 나가야 되기 때문이다.
예를 들어 다음 과 같은 배열이 있다고 가정해보자.
[0,1,2,3,4,5,6]
여기서 5번째 인덱스의 경우 앞에서 부터 뽑는 경우의 수가 [0,2,5] 혹은 [0,3,5], [1,3,5] 이런식으로 여러가지의 경우의 수가 존재한다.
따라서 5를 선택하기 바로 직전의 값 중에서 최대가 되는 결과로 항상 갱신해야한다.
그리고 한가지 더 고려해야 할것이 0을 선택할 경우 6을 선택하지 못하게 된다.
따라서 0번째 인덱스를 고를 경우 for문의 길이가 0 ~ (length - 2)가 되고
1번째 인덱스를 고를 경우 for문의 길이가 1 ~ (length - 1)이 된다.
따라서 dp 테이블의 경우도 0번째부터 시작하는것과 1번째부터 시작하는 것 2개를 설정해야 한다.
그러면 dp는 어떻게 갱신할까?
i번째 인덱스를 보고 있는 상황이라고 가정해보자
sticker = [.....,x,x,13(i)]
dp = [.....,10( i - 2),12(i - 1)]
이런식으로 되어 있다고 할때
dp[i] 는 2가지의 경우가 있다.
dp[ i -2]( 10 ) + 현재 sticker[i](13)가 되는 상황과 -> 현재 스티커를 선택하는 상황
dp[i - 1]을 고르고 현재 스티커는 선택하지 않는 상황이다.-> 현재 스티커를 선택하지 않는 상황
이때 2개중의 최댓값이 되는 것을 dp[i]로 설정하면 된다.
이런식으로 범위를 살짝 달리하여 2개의 dp를 기록해 나가면 된다.
def solution(sticker):
size = len(sticker)
if size == 1:
return sticker[0]
dp1 = [0] * size
dp1[0] = sticker[0] # 0번째 인덱스 부터 시작하는경우 dp의 0과 1 번째 인덱스는 sticker[0]으로 고정된다.
dp1[1] = sticker[0]
dp2 = [0] * size
dp2[0] = 0 #1번째 인덱스 부터 시작하는 경우 0번째 스티커는 접근이 불가하다
dp2[1] = sticker[1]
#2로 시작하는 경우는 이미 1번째 혹은 0번째는 뗏다고 가정하고 시작하기 때문이다.
#위에서 dp의 값을 미리 설정하는 이유이다.
#0번째 부터 시작하는 경우 맨 마지막 스티커는 떼지 못한다
for i in range(2, size - 1):
dp1[i] = max(dp1[i - 2] + sticker[i], dp1[i - 1])
# 1번째 부터 시작하는 경우 맨 마지막 스티커는 뗄수 있다.
for i in range(2, size):
dp2[i] = max(dp2[i - 2] + sticker[i], dp2[i - 1])
answer = max(dp1[size - 2], dp2[size - 1])
return answer
'알고리즘' 카테고리의 다른 글
| [프로그래머스] - N_Queen[파이썬] (1) | 2023.03.15 |
|---|---|
| [프로그래머스] - 디스크컨트롤러[인터벌 스케쥴링][파이썬] (0) | 2023.03.10 |
| [프로그래머스] - N으로표현[파이썬] (0) | 2023.03.09 |
| [프로그래머스] - 등대 [파이썬] (0) | 2023.03.07 |
| [프로그래머스] - 순위 [파이썬][플로이드 와셜] (1) | 2023.03.06 |